数学,图像,以及经济内涵
方才,我正在复习昨天学习的经济学课程。为了理解过程中学习到的概念,进行了大概30分钟的深度思考(说是深度思考,不过是我个人过度思考这一恶习的延申),而这次彻底领悟的经验,让我对经济学和数学似乎又有了新的理解。
我当时正在复习的概念是资本(Capital,K)的边际产量和劳动(Labor,L)的边际产量。在经济学的世界里,我们有以下三个假设:
- $MP_k\ge0$, $MP_L\ge0$,即资本和劳动的生产偏微分应大于等于零,其经济学内涵就是生产要素的增多必然导致产出的增长。
- 边际产量递减,即越多的某一生产要素,其边际产量减少。
- K与L为互补要素,一起使用能提升产量。
如果这是初级的经济学导论,那么只要简单记住字面意思就可以了,不过作为中级经济学课程,我们需要通过数学来计算出生产方程的利润最大化,因此,我们需要对上述概念有更深入的探讨。
我个人倾向于从三个维度来解释,分别是数学方程、图像、以及经济内涵。
从数学方面来考量,我们通过公式得知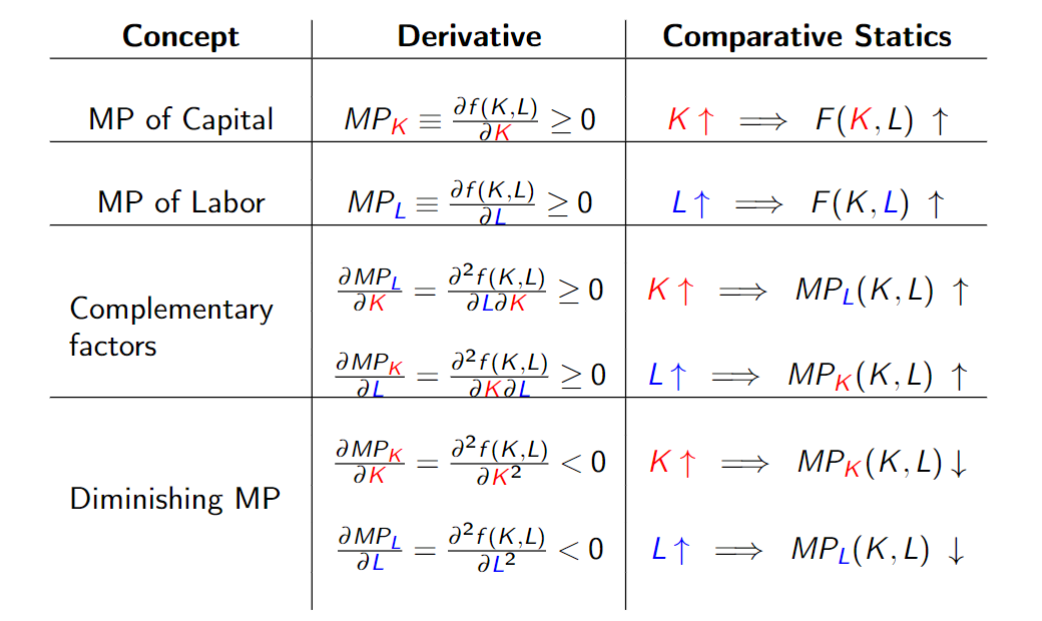
只看偏微分的结果是很干瘪的,因为这只是数学对文字的翻译而已,我们需要在经济学的背景下了解其所以然,不过更重要的是,为什么数学会给出这样的结果。图像就起到了很大的帮助。而这些都是我脑海中的画面,所以我也截不了图。
首先,条件一内含以下假设:在一个3D平面中,包含产量Q,资本K,劳动L三个变量,而不同KL的组合会提供唯一的Q。因此,当我们假设$MP_k\ge0$, $MP_L\ge0$时,实际上是指图像在$K>0$,$L>0$时单调递增。
如此一来,如果单一从$K$轴看去,或是从$L$轴看,面对的应该是单调递增的曲线,结合假设二,曲线应当斜率递减。
通过上述,应该可以得出上图中的结论:
- 每增加一单位K均可导致Q的增加,即$q=f(K,L)>0$;
- 对于产量方程求不同轴的二次偏导时,我们可以明显看出,对于图像上任意一点,其K轴与L轴皆为递增。因此,K与L经济效益上互补。
- 对于单个轴求二次偏导,其图像向下突起,因此加速度为负,一阶导增速减缓,代表边际产量递减。
得图像者得数学,得图像者得经济。